算法-图-查找路径

力扣题目：1971. 寻找图中是否存在路径 - 力扣（LeetCode）

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径 ，则返回 true，否则返回 false 。

示例 1：

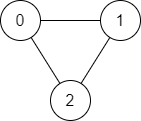
输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2 
- 0 → 2

示例 2：

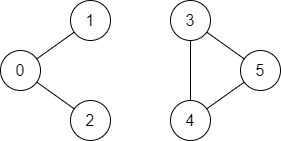
输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

提示：

  • 1 <= n <= 2 * 10^5
  • 0 <= edges.length <= 2 * 10^5
  • edges[i].length == 2
  • 0 <= ui, vi <= n - 1
  • ui != vi
  • 0 <= source, destination <= n - 1
  • 不存在重复边
  • 不存在指向顶点自身的边

算法如下

  1. package com.dji.sample.accessControlDf;
  2.  
  3. import java.util.ArrayDeque;
  4. import java.util.ArrayList;
  5. import java.util.List;
  6. import java.util.Queue;
  7.  
  8. public class Solution {
  9.     //用DFS深度优先遍历解决,
  10.     public  boolean validPath(int n, int[][] edges, int source, int destination) {
  11.         //标记数组
  12.         boolean []flagArr=new boolean[n];
  13.         //构造邻接矩阵,内存会超出限制
  14. //        int[][] vG=new int [n][n];
  15. //        //这样构造需要的存储空间太大了
  16. //        for(int i=0;i<edges.length;i++)
  17. //        {
  18. //            vG[edges[i][0]][edges[i][1]]=1;
  19. //            vG[edges[i][1]][edges[i][0]]=1;
  20. //        }
  21.         List<Integer>[] adj = new List[n];
  22.         for (int i = 0; i < n; i++) {
  23.             adj[i] = new ArrayList<Integer>();
  24.         }
  25.         //添加无向图
  26.         for (int[] edge : edges) {
  27.             int x = edge[0], y = edge[1];
  28.             adj[x].add(y);
  29.             adj[y].add(x);
  30.         }
  31.  
  32. //   dfs     dfsSearch(vG,source,flagArr,destination);
  33.         //用bfs
  34.         //队列存储标记点
  35.         Queue<Integer> queue=new ArrayDeque<>();
  36.         //出发点入队
  37.         queue.offer(source);
  38. //        bfsSearch(vG,flagArr,source,destination,queue);
  39.         bfs(adj,source,destination,flagArr,queue);
  40.         return flagArr[destination];
  41.     }
  42.     //DFS深度优先递归，内存、时间会超出限制
  43.     public void dfsSearch(int [][] vG,int v,boolean[] flagArr,int destination)
  44.     {
  45.         //节点v被访问
  46.         flagArr[v]=true;
  47.         //优化：如果访问到目的地结束
  48.         if(destination==v)
  49.         {
  50.             return;
  51.         }
  52.         for(int i=0;i<vG.length;i++)
  53.         {
  54.             if(vG[v][i]==1&&flagArr[i]==false)
  55.             {
  56.                 //递归访问邻居节点，如果没有就回退
  57.                 dfsSearch(vG,i,flagArr,destination);
  58.             }
  59.         }
  60.     }
  61.     public void bfsSearch(int[][] vG, boolean[] flagArr,int v, int destination, Queue<Integer> queue)
  62.     {
  63.         flagArr[v]=true;
  64.  
  65.         while (!queue.isEmpty())
  66.         {
  67.             //队头出队
  68.             int vHead=queue.poll();
  69.             //访问队头所在的邻接矩阵
  70.             for(int i=0;i<vG.length;i++)
  71.             {
  72.                 if(vG[vHead][i]==1&&flagArr[i]==false)
  73.                 {
  74.                     //入队
  75.                     queue.offer(i);
  76.                     //标记为访问
  77.                     flagArr[i]=true;
  78.                     if(i==destination)
  79.                     {
  80.                         return;
  81.                     }
  82.                 }
  83.             }
  84.         }
  85.  
  86.     }
  87.     public void bfs(List<Integer>[] adj,int source,int destination,boolean[]flagArr,Queue<Integer> queue )
  88.     {
  89.         //队头已经被访问
  90.         flagArr[source]=true;
  91.         while (!queue.isEmpty())
  92.         {
  93.             //队头出队
  94.             int vHead= queue.poll();
  95.             //访问队头所在的邻接矩阵
  96.             List<Integer> nodeList=adj[vHead];
  97.             for(Integer i:nodeList)
  98.             {
  99.                 if(flagArr[i]==false)
  100.                 {
  101.                     flagArr[i]=true;
  102.                     //入队
  103.                     queue.offer(i);
  104.                     if(i==destination)
  105.                     {
  106.                         return;
  107.                     }
  108.                 }
  109.             }
  110.  
  111.         }
  112.  
  113.     }
  114.  
  115. }

注：本文转载自blog.csdn.net的程序员南飞的文章"https://blog.csdn.net/silent702366/article/details/145848253"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！