代码人生|【机器学习】朴素贝叶斯算法：原理剖析与实战应用

引言

朴素贝叶斯算法就像是一位善于从经验中学习的侦探，根据已有的线索来推断未知事件的概率。这是一种基于概率论的分类算法，以贝叶斯定理为基础，却做了一个"朴素"的假设：认为所有特征彼此独立。虽然这个假设在现实中很少完全成立（就像假设一个人喜欢鞋子与喜欢包包无关）。尽管如此，该算法在实际应用中仍然表现出色，特别是在文本分类、垃圾邮件过滤和情感分析等领域，它简单高效的特点使其成为机器学习的"常青树"。

贝叶斯定理：故事从这里开始

假设你是一位医生，一位患者的检测结果呈阳性。要判断他真的患病的概率，你需要考虑：检测的准确性、疾病的普遍程度等因素。这正是贝叶斯定理所解决的问题！

贝叶斯定理的公式如下：

P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}

用日常语言解释：

$P(A|B)$ 是"已知B发生后，A发生的概率"（如：检测为阳性后，真实患病的概率）
$P(B|A)$ 是"已知A发生后，B发生的概率"（如：患病者检测呈阳性的概率）
$P(A)$ 是"A发生的初始概率"（如：人群中患病率）
$P(B)$ 是"B发生的总体概率"（如：检测结果为阳性的总体概率）

朴素贝叶斯：贝叶斯定理的实用简化版

想象一下，你在给电子邮件分类。看到"免费"、"优惠"这样的词，你可能会怀疑是垃圾邮件；看到"会议"、"报告"，则可能是工作邮件。朴素贝叶斯正是模仿这种思考过程！

核心思想

朴素贝叶斯的目标是：给定一组特征（如邮件中的词语），预测它属于哪个类别（如垃圾邮件还是正常邮件）。

用数学公式表达：

P(类别|特征) = \frac{P(特征|类别) \times P(类别)}{P(特征)}

由于我们只关心哪个类别的概率最大，而对于同一组特征，分母 $P(特征)$ 是固定的，因此简化为：

最可能的类别 = \arg\max_{类别} [P(特征|类别) \times P(类别)]

这里的"朴素"体现在一个简化假设：所有特征之间相互独立。这就像假设一封邮件中"免费"和"优惠"这两个词的出现互不影响。虽然这在现实中不太可能，但这个假设大大简化了计算：

P(所有特征|类别) = P(特征1|类别) \times P(特征2|类别) \times ... \times P(特征n|类别)

朴素贝叶斯的三种"口味"

就像冰淇淋有不同口味，朴素贝叶斯也有三种常见变体，适用于不同类型的数据：

1. 高斯朴素贝叶斯：处理连续数值

适用场景：身高、体重、温度等连续数值特征。

它假设每个类别下的特征值服从正态分布（钟形曲线）。例如，男性和女性的身高分别服从不同参数的正态分布。

2. 多项式朴素贝叶斯：处理出现次数

适用场景：文本分析中的词频统计。

它关注特征（如单词）出现的次数。比如，垃圾邮件中"优惠"出现的频率比正常邮件高。

3. 伯努利朴素贝叶斯：处理是否出现

适用场景：特征只关注是否出现，不关注出现次数。

比如，分析一封邮件是否包含某些关键词，而不关心这些词出现了几次。

朴素贝叶斯算法流程图

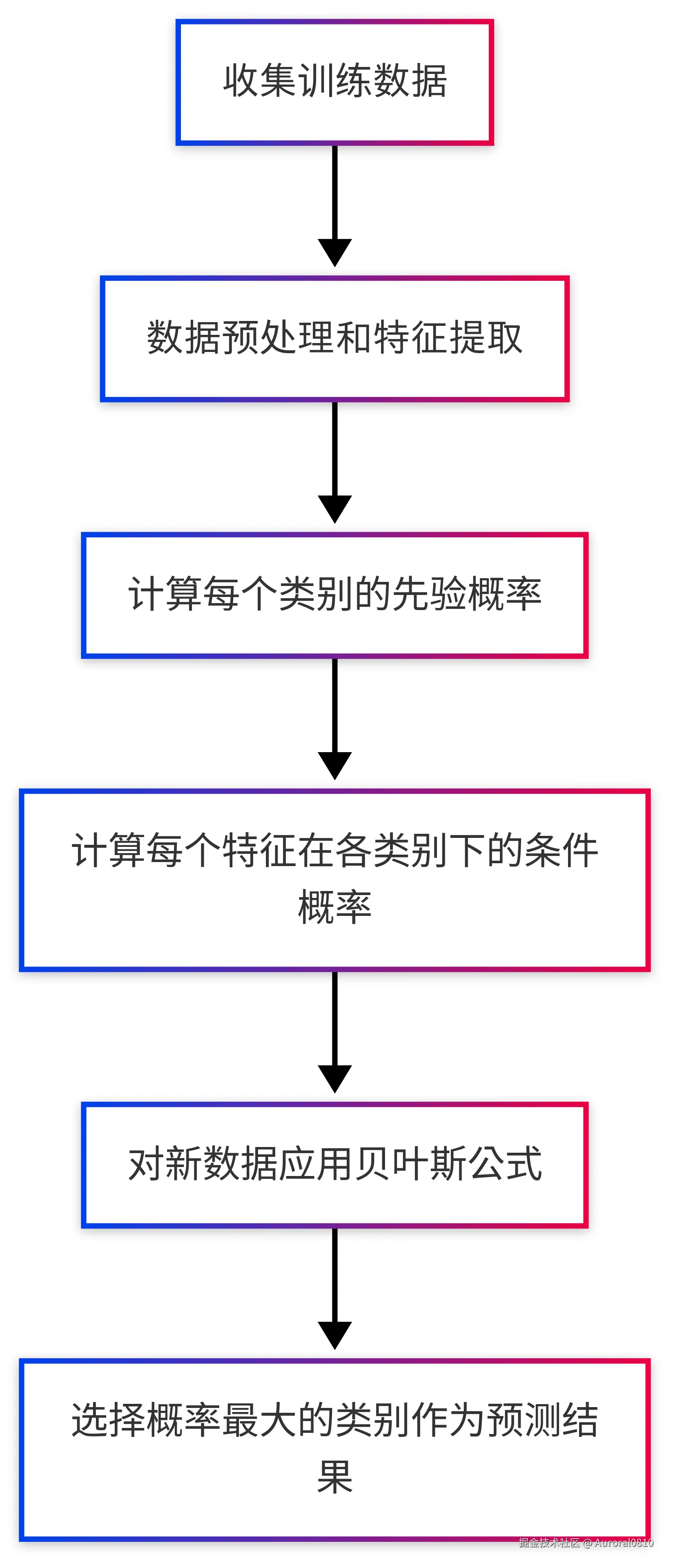
拉普拉斯平滑：解决"零概率"危机

想象这种情况：你的训练数据中，"比特币"这个词从未在正常邮件中出现过。按照概率计算，P(比特币|正常邮件) = 0。这意味着，一旦新邮件中出现"比特币"，算法就会断定它不可能是正常邮件，这显然太极端了！

拉普拉斯平滑（又称"加一平滑"）通过在分子和分母都加上一个小数值，避免了零概率的出现：

P(特征|类别) = \frac{特征在该类别中出现的次数 + 1}{该类别的特征总数 + 特征种类总数}

这就像是给每个特征一个"出场机会"，即使它在训练数据中从未出现过。

实际案例详解：垃圾邮件过滤器

背景

我们将构建一个简单的垃圾邮件过滤器，就像你邮箱中的那个，但更简单易懂。

训练数据

假设我们有5封训练邮件：

内容	类别
"优惠促销免费赠品"	垃圾邮件
"会议通知项目进度"	正常邮件
"免费获取限时优惠"	垃圾邮件
"周报提交项目计划"	正常邮件
"团队会议工作总结"	正常邮件

步骤分解（小白也能懂的计算过程）

第一步：计算每类邮件的基础概率

垃圾邮件：2/5 = 40%
正常邮件：3/5 = 60%

第二步：统计词语出现情况 词汇表：{"优惠", "促销", "免费", "赠品", "会议", "通知", "项目", "进度", "获取", "限时", "周报", "提交", "计划", "团队", "工作", "总结"}

第三步：计算每个词在各类邮件中的出现概率（加一平滑） 例如：

在垃圾邮件中，"优惠"出现2次，总词数8个，词表大小16。 P(优惠|垃圾) = (2+1)/(8+16) = 3/24 = 0.125
在正常邮件中，"项目"出现3次，总词数12个，词表大小16。 P(项目|正常) = (3+1)/(12+16) = 4/28 ≈ 0.143

第四步：对新邮件"团队优惠项目促销"进行分类

计算它是垃圾邮件的概率： P(垃圾|新邮件) ∝ 0.4 × 0.042(团队) × 0.125(优惠) × 0.042(项目) × 0.083(促销) ≈ 7.35×10⁻⁶

计算它是正常邮件的概率： P(正常|新邮件) ∝ 0.6 × 0.107(团队) × 0.036(优惠) × 0.143(项目) × 0.036(促销) ≈ 10.01×10⁻⁶

由于正常邮件的概率更高，所以我们将这封邮件分类为正常邮件。

Python实战：十行代码实现垃圾邮件过滤

下面是一个简单实用的Python实现：


python
 代码解读
复制代码
import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score, classification_report

# 准备数据：10封邮件样本
emails = [
    "优惠促销 免费赠品",
    "会议通知 项目进度",
    "免费获取 限时优惠",
    "周报提交 项目计划",
    "团队会议 工作总结",
    "限时折扣 免费试用",  # 你可以加入更多样本
    "项目总结 团队协作",
    "促销活动 抽奖优惠",
    "工作安排 会议记录",
    "免费课程 限时报名"
]

# 标签：0=正常邮件，1=垃圾邮件
labels = [1, 0, 1, 0, 0, 1, 0, 1, 0, 1]

# 步骤1：划分训练集和测试集（70%用于训练，30%用于测试）
X_train, X_test, y_train, y_test = train_test_split(
    emails, labels, test_size=0.3, random_state=42
)

# 步骤2：将文本转换为词频特征（词袋模型）
vectorizer = CountVectorizer()
X_train_counts = vectorizer.fit_transform(X_train)
X_test_counts = vectorizer.transform(X_test)

# 步骤3：训练朴素贝叶斯模型（使用多项式变体，适合文本）
model = MultinomialNB(alpha=1.0)  # alpha=1.0表示使用拉普拉斯平滑
model.fit(X_train_counts, y_train)

# 步骤4：在测试集上评估模型
y_pred = model.predict(X_test_counts)
accuracy = accuracy_score(y_test, y_pred)
report = classification_report(y_test, y_pred, target_names=["正常邮件", "垃圾邮件"])

print(f"模型准确率: {accuracy:.2f}")
print("\n详细评估报告:")
print(report)

# 步骤5：尝试对新邮件进行分类
new_emails = ["团队优惠 项目促销", "免费获取 限时折扣", "项目会议 工作安排"]
new_counts = vectorizer.transform(new_emails)
predictions = model.predict(new_counts)
probabilities = model.predict_proba(new_counts)

# 输出预测结果及概率
print("\n新邮件分类结果:")
for email, prediction, proba in zip(new_emails, predictions, probabilities):
    category = "垃圾邮件" if prediction == 1 else "正常邮件"
    print(f"'{email}' → {category}")
    print(f"  - 是正常邮件的概率: {proba[0]:.2f}, 是垃圾邮件的概率: {proba[1]:.2f}")

朴素贝叶斯算法的优缺点

优点

速度飞快：训练和预测速度比大多数算法都快，适合实时应用
小数据也能行：即使训练样本不多，效果也不错
高维数据处理好手：特别适合文本分类这种特征维度高的场景
增量学习支持：可以不断学习新数据，无需重新训练整个模型
解释性强：预测结果背后的原因容易解释，不像深度学习那样"黑盒"

缺点

特征独立性假设过强：现实世界中特征往往相互关联
数据不平衡敏感：如果某类数据样本远多于其他类，可能产生偏见
连续数值处理不够精细：对连续特征的处理不如一些专门算法
零概率问题：需要使用平滑技术来避免

常见Q&A

Q：为什么叫"朴素"贝叶斯？
A：因为它做了一个朴素（naive）的假设，认为所有特征之间相互独立，这在实际中很少成立，但简化了计算并且效果出人意料地好。

Q：什么场景最适合使用朴素贝叶斯？
A：文本分类（如垃圾邮件过滤、情感分析、新闻分类）、医疗诊断、推荐系统等。特别是当特征较多且训练数据有限时，朴素贝叶斯往往表现优秀。

Q：如何处理连续值特征？
A：可以使用高斯朴素贝叶斯，或者将连续值离散化（分箱）后使用多项式朴素贝叶斯。

Q：如何提高朴素贝叶斯的准确率？
A：可以尝试更好的特征选择、调整平滑参数、结合其他模型形成集成学习等方法。

结语

朴素贝叶斯算法是机器学习中的"老前辈"，它用简单的概率计算就能解决复杂的分类问题。虽然它基于一个"天真"的假设，但在实际应用中却屡屡证明其价值。它就像是机器学习世界中的"瑞士军刀"—简单、快速、多用途。对于初学者来说，朴素贝叶斯是理解概率模型的绝佳起点。

引言