数学|[c语言日记]动态规划入门：杨辉三角

在这里插入图片描述

【作者主页】siy2333
【专栏介绍】⌈c语言日寄⌋：这是一个专注于C语言刷题的专栏，精选题目，搭配详细题解、拓展算法。从基础语法到复杂算法，题目涉及的知识点全面覆盖，助力你系统提升。无论你是初学者，还是进阶开发者，这里都能满足你的需求！
【食用方法】1.根据题目自行尝试 2.查看基础思路完善题解 3.学习拓展算法
【Gitee链接】资源保存在我的Gitee仓库：https://gitee.com/siy2333/study

文章目录

前言
一、题目引入
- 杨辉三角的构造规则
二、什么是动态规划
三、功能规划
四、题目解答
- 代码解析
五、注意事项
总结

前言

在C语言的学习过程中，动态规划是一个非常重要且实用的概念，可以帮助我们解决复杂的数学问题。今天，我们就以杨辉三角为例，探讨动态规划在C语言中的应用。

一、题目引入

杨辉三角，又称帕斯卡三角，是一种经典的组合数学问题。它以一种三角形的形式展示，每一行的数字都是由上一行的数字通过简单的加法运算得到的。

杨辉三角的构造规则

每一行的第一个和最后一个数字都是1。
从第三行开始，每一行的中间数字等于上一行的相邻两个数字之和。
例如，杨辉三角的前几行如下所示：

杨辉三角的构造规则简单，但如何高效地实现它，却是一个有趣的问题。接下来，我们将通过动态规划算法来破解杨辉三角。

二、什么是动态规划

动态规划（Dynamic Programming，简称DP）是一种用于解决多阶段决策问题的算法思想。它通过将复杂问题分解为多个相对简单的子问题，并通过求解子问题来逐步构建最终的解决方案。

动态规划的核心在于“记忆化”和“重用”，即通过存储已经解决的子问题的解，避免重复计算，从而提高算法的效率。

基本要素

最优子结构
一个复杂问题的最优解可以由其子问题的最优解组合而成。这是动态规划的基础，意味着问题可以被分解为多个子问题，并且这些子问题的解可以组合成原问题的解。
重叠子问题
在求解过程中，相同的子问题会被多次计算。动态规划通过存储这些子问题的解（通常使用一个表格），避免重复计算，从而提高效率。
状态转移方程
描述如何从子问题的解推导出原问题的解。状态转移方程是动态规划的核心，它定义了子问题之间的关系。

应用场景

动态规划广泛应用于以下领域：

组合优化问题：如背包问题、最长公共子序列等。
路径规划问题：如最短路径问题、旅行商问题等。
资源分配问题：如生产计划、资源分配等。

动态规划与递归的区别

动态规划和递归都是解决问题的方法，但它们有本质的区别：

递归：通过将问题分解为更小的子问题，递归地求解子问题。递归可能会导致大量的重复计算，相对而言，效率较低。
动态规划：通过存储子问题的解，避免重复计算，从而提高效率。动态规划通常使用迭代的方式实现，更适合解决具有重叠子问题的优化问题。

动态规划的实现步骤

定义状态：确定问题的子问题，并定义状态变量来表示子问题的解。
建立状态转移方程：描述如何从子问题的解推导出原问题的解。
初始化状态：确定初始状态的值，通常是最简单的子问题的解。
计算顺序：确定计算子问题的顺序，通常从小到大计算。
存储状态：使用数组或表格存储子问题的解，避免重复计算。

动态规划的优势

高效性：通过存储子问题的解，避免重复计算，提高算法效率。
可扩展性：动态规划可以处理复杂的多阶段决策问题，适用于多种应用场景。
灵活性：动态规划可以根据问题的不同需求进行调整和优化。

接下来，我们将通过杨辉三角的实现，具体的理解动态规划的应用。

三、功能规划

杨辉三角输出程序的功能主要包括以下几个方面：

初始化数组
我们需要一个数组来存储每一行的数字。由于杨辉三角的每一行数字数量逐渐增加，因此我们通常需要一个足够大的数组来存储所有行的数字。
动态规划算法
动态规划的核心思想是将问题分解为多个子问题，并通过解决子问题来逐步构建最终的解决方案。

在杨辉三角中，每一行的数字可以通过上一行的数字计算得到，这正是动态规划的应用场景。

可视化输出
我们需要将杨辉三角的每一行输出到屏幕上，方便验证算法。
优化与扩展
在实现基本功能的基础上，我们还可以对代码进行优化，例如减少内存使用量、提高运行效率等。

四、题目解答

#include 
#include 

#define SIZE (20 + 1)
//常量，用于控制输出的数组大小
//实际输出行数为20行，+1是为了确保第一行按照公式正确计算

int main() {
    int arr[SIZE];
    int arr1[SIZE];//数组定义
    memset(arr, 0, sizeof(int) * SIZE);
    arr[1] = 1;
    memset(arr1, 0, sizeof(int) * SIZE);//数组初始化

    int coo;//中间值，坐标的缩写，用于记录目前打印的位置

    printf("1\n");//输出第一行
    for (int i = 0; i < SIZE - 2; i++) {
        coo = 1;
        memset(arr1, 0, sizeof(int) * SIZE);//初始化
        while (arr[coo] != 0) {
            arr1[coo] = arr[coo] + arr[coo - 1];//记录当前正在输出行的数据
            //每一行的数字可以通过上一行的数字计算得到
            printf("%d ", arr[coo] + arr[coo - 1]);
            coo++;
        }
        arr1[coo] = arr[coo] + arr[coo - 1];
        printf("%d\n", arr[coo] + arr[coo - 1]);
        coo++;
        
        for (int i = 0; i < coo; i++) {
        	//将目前行的数据更新到“上一行数组”
            arr[i] = arr1[i];
        }
    }

    return 0;
}

运行结果如下：
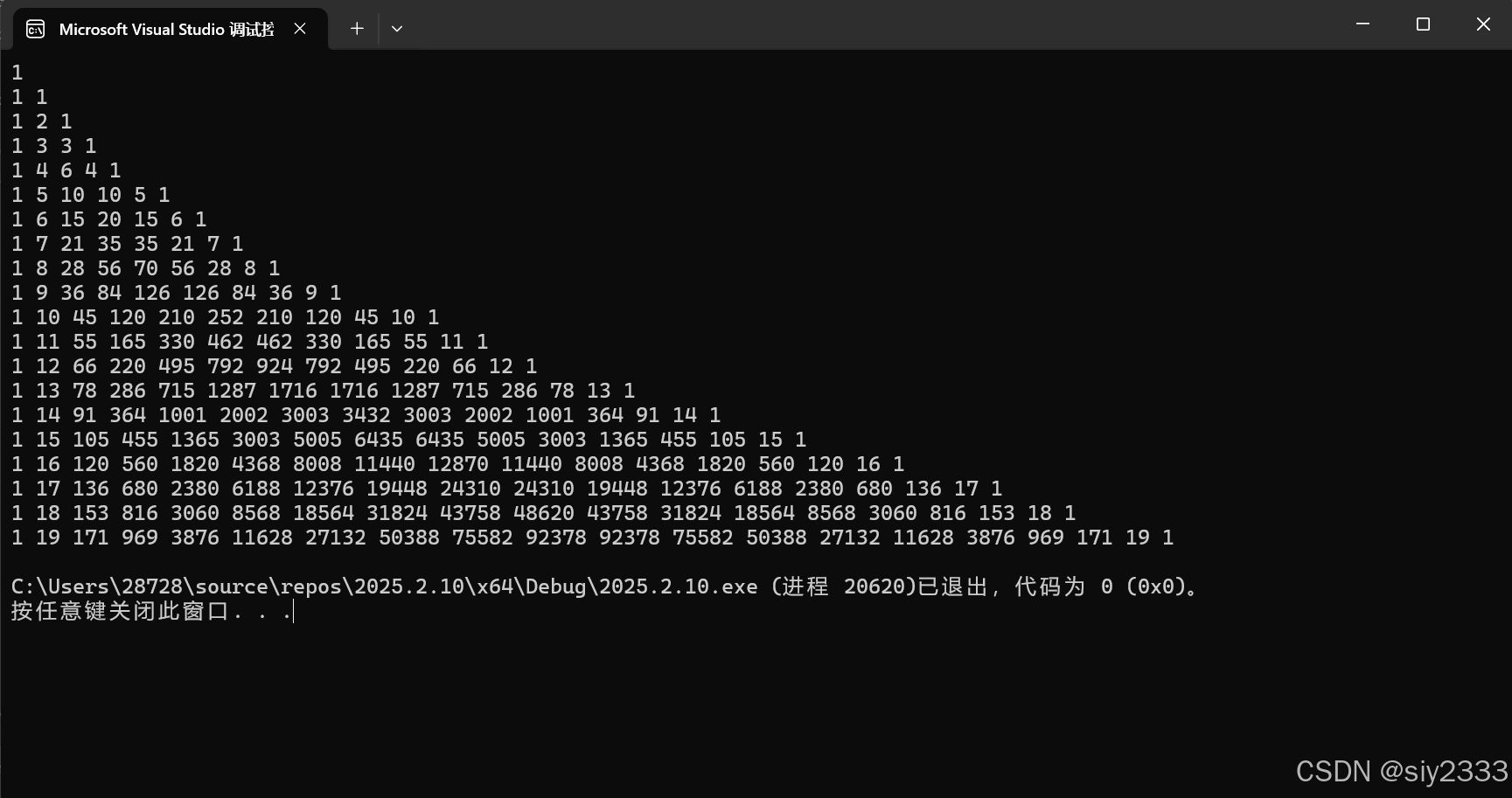
在这里插入图片描述

代码解析

数组初始化
我们定义了两个数组arr和arr1，分别用于存储当前行和下一行的数字。
使用memset函数将数组初始化为0，确保数组中的所有元素都为0。
将arr[1]初始化为1，表示杨辉三角的第一行。
动态规划算法
使用一个for循环来逐行计算杨辉三角的数字。
在每一行中，使用while循环来计算当前行的数字，并将其存储在arr1中。
每次计算完成后，将arr1中的值复制回arr，以便下一行的计算。
输出结果
在计算每一行的数字时，使用printf函数将数字输出到屏幕上。

五、注意事项

在实现杨辉三角的动态规划算法时，需要注意以下几个问题：

数组大小
由于杨辉三角的行数可以非常大，因此我们需要确保数组的大小足够大，以避免溢出。我们通过定义一个常量SIZE，控制输出的大小，同时保证定义的数组大小匹配。
边界情况
为了计算第一行，我们将SIZE定义为输出“行数+1”，并且将arr[0]始终保持为0，使得通过公式arr1[coo] = arr[coo] + arr[coo - 1]，我们可以正确的运算出第一行的值，即始终为1。
内存管理
我们需要确保在程序运行过程中正确地分配和释放内存，以避免数组越界。我们在for循环中使用SIZE-2，以避免数组越界访问。
性能优化
虽然杨辉三角的计算相对简单，但在处理大量行数时，性能优化是必要的，所以，相较于常规的递归法，我们可以使用本文介绍的动态规划法。

总结

杨辉三角是一个经典的动态规划问题，通过C语言实现可以很好地展示动态规划的思想和方法。在实现过程中，需要注意数组大小、边界条件、内存管理和性能优化等问题。
希望这篇文章能帮助你更好地理解和实现杨辉三角的动态规划算法。如果你对动态规划或其他C语言问题感兴趣，那么，关注窝，每三天至少更新一篇优质c语言题目详解~

[专栏链接QwQ] :⌈c语言日寄⌋CSDN
[关注博主ava]：siy2333
感谢观看~ 我们下次再见!!