1 纵向小扰动方程

系统纵向小扰动方程的状态空间方程为
$\dot{x}=Ax+Bu$
$y=Cx+Du$
式中：
$$x=\left(\begin{array}{c}{v}_T\\ \alpha \\ \theta \\ q\\ h\end{array}\right)$$
$$u=\left(\begin{array}{c}{\delta }_t\end{array}\right)$$
使用参考文献[1]中Example3.8.5的模型：

2 编写MATLAB程序

%% ACS_E3_8_5
% Liang
% 20250116

% Clear
clear;

% 定义系统矩阵
A = [-1.6096E-02, 1.8832E+01, -3.2170E+01, 0.0000E+00, 5.4000E-05;
    -1.0189E-03, -6.3537E-01, 0.0000E+00, 1.0000E+00, 3.7000E-06;
    0.0000E+00, 0.0000E+00, 0.0000E+00, 1.0000E+00, 0.0000E+00;
    1.0744E-04, -7.7544E-01, 0.0000E+00, -5.2977E-01, -4.1000E-07;
    0.0000E+00, -2.5000E+02, 2.5000E+02, 0.0000E+00, 0.0000E+00];

B = [9.9679E+00;
    -6.5130E-03;
    0.0000E+00;
    2.5575E-02;
    0.0000E+00];

C = eye(5);

D = zeros(5, 1);

% 使用ss函数建立状态空间模型
g = ss(A, B, C, D);

% 显示状态空间模型
disp(g);

% 状态空间转换成传递函数
[num1, den1] = ss2tf(A, B, C, D, 1);
num1q = num1(1,:);
g_open = tf(num1q, den1);
% clsys1 = feedback(plant1, 1);

% Bode图
figure(25010301)
bode(num1q, den1);
grid minor;
grid on;

% Save
set(gcf, 'Position', [50, 50, 4*250, 3*250]);
saveas(gcf,'ACS_E3_8_5_bode','png');

% 根轨迹
figure(25010302)
rlocus(g_open);
grid minor;
grid on;

% Save
set(gcf, 'Position', [50, 50, 4*250, 3*250]);
saveas(gcf,'ACS_E3_8_5_rlocus','png');

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55

3 计算结果

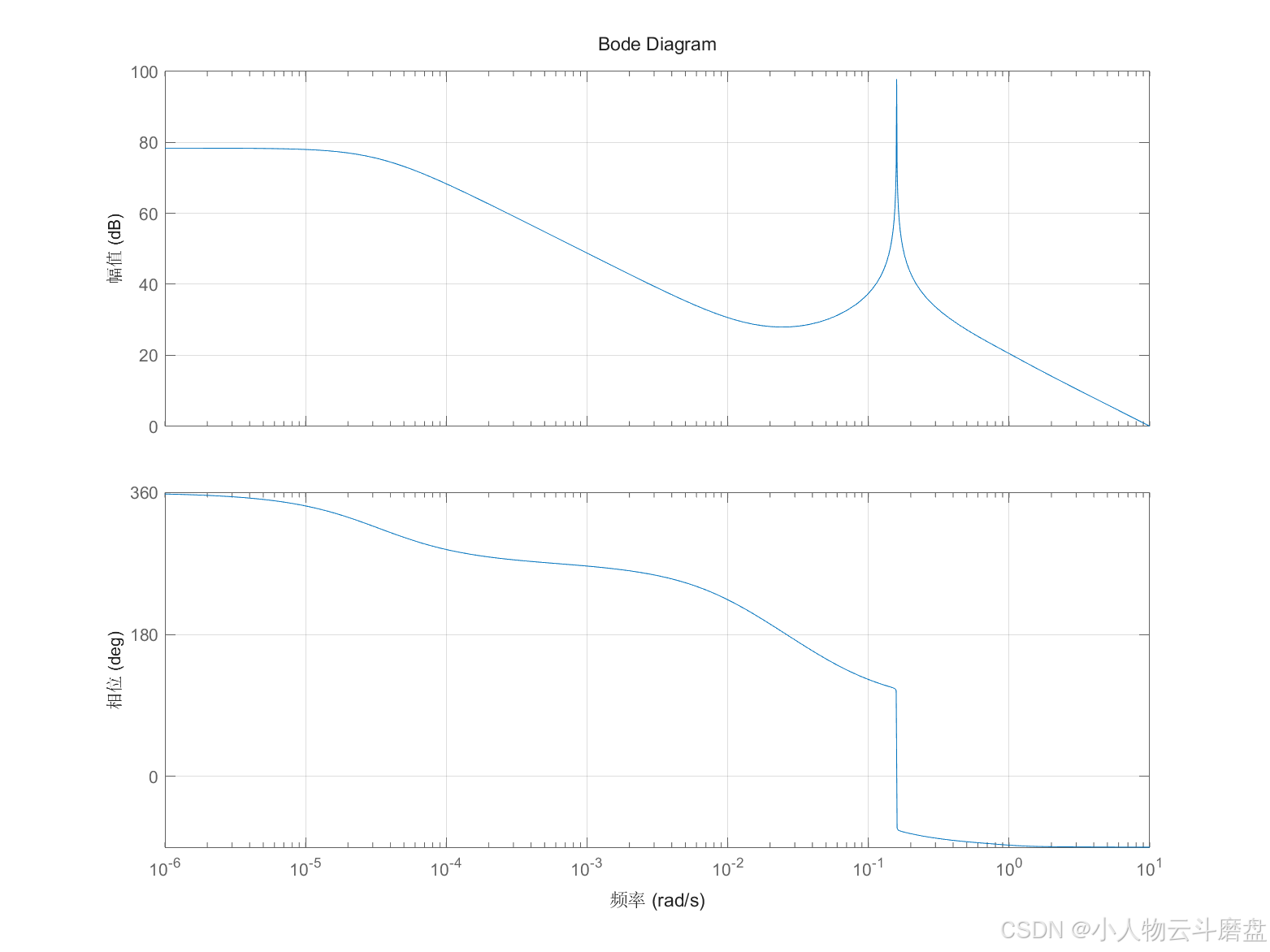
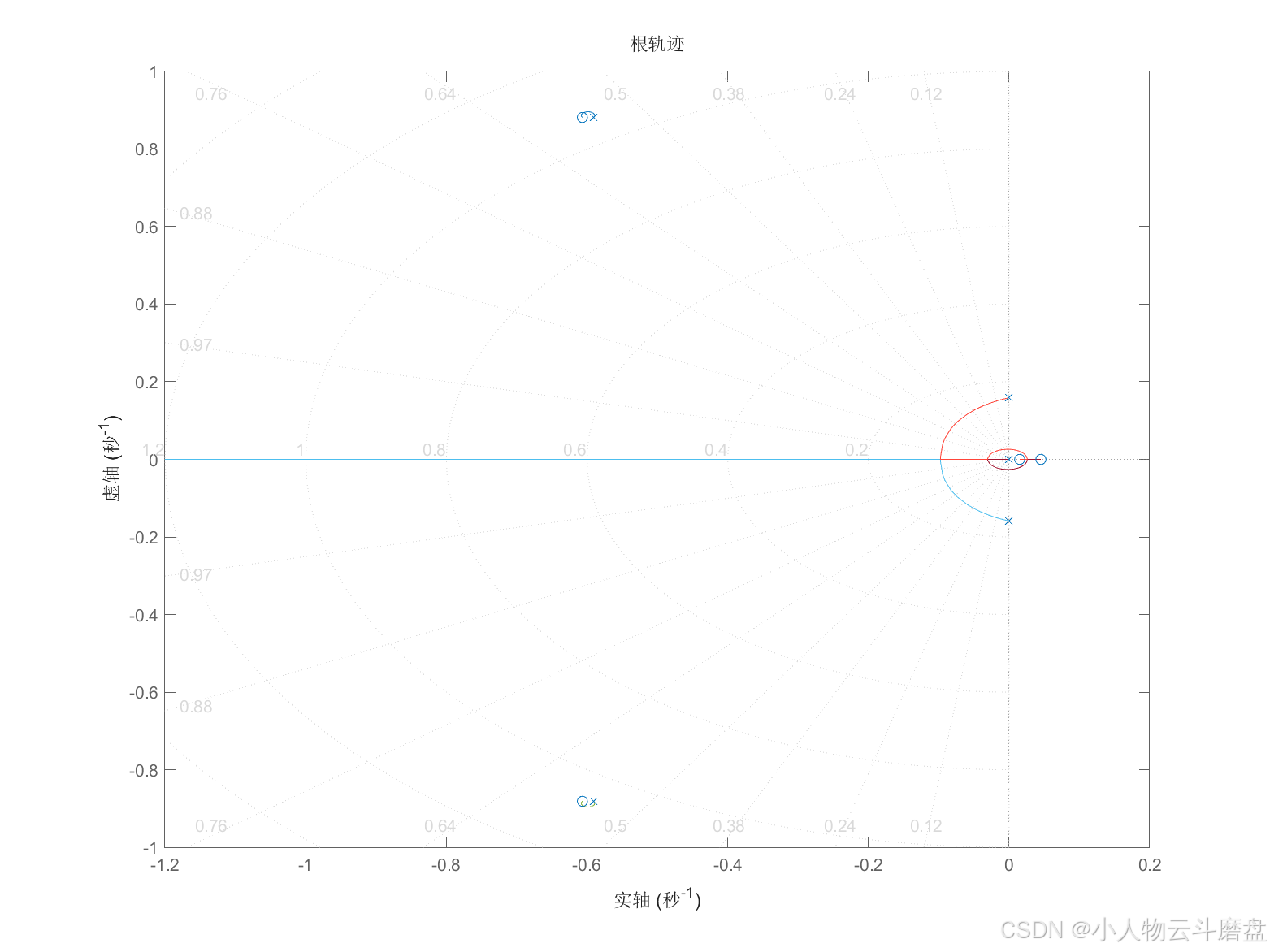
[1] Brian L. Stevens, Frank L. Lewis, Eric N. Johnsson. Aircraft Control and Simulation[M]. 3rd ed. New Jersey: John Wiley & Sons, Inc, 2016: 211.