力扣中等难度热题——长度为K的子数组的能量值

目录

题目链接：3255. 长度为 K 的子数组的能量值 II - 力扣（LeetCode）

题目描述

示例

提示：

解法一：通过连续上升的长度判断

Java写法：

C++写法：

 相比与Java写法的差别

运行时间

时间复杂度和空间复杂度

时间复杂度：

空间复杂度：

解法二：双指针+极限优化

优化前

Java写法：

优化前运行时间

优化后

优化的思路与实现：

Java写法：

C++写法：

优化分析：

运行时间

时间复杂度和空间复杂度

时间复杂度：

空间复杂度：

总结

解法一：通过连续上升的长度判断

解法二：双指针 + 极限优化

对比：

题目链接：3255. 长度为 K 的子数组的能量值 II - 力扣（LeetCode）

注：下述题目描述和示例均来自力扣

题目描述

给你一个长度为 n 的整数数组 nums 和一个正整数 k 。

一个数组的 能量值 定义为：

  • 如果 所有 元素都是依次 连续 且 上升 的，那么能量值为 最大 的元素。
  • 否则为 -1 。

你需要求出 nums 中所有长度为 k 的 子数组的能量值。

请你返回一个长度为 n - k + 1 的整数数组 results ，其中 results[i] 是子数组 nums[i..(i + k - 1)] 的能量值。

示例

示例 1：

输入：nums = [1,2,3,4,3,2,5], k = 3

输出：[3,4,-1,-1,-1]

解释：

nums 中总共有 5 个长度为 3 的子数组：

  • [1, 2, 3] 中最大元素为 3 。
  • [2, 3, 4] 中最大元素为 4 。
  • [3, 4, 3] 中元素 不是 连续的。
  • [4, 3, 2] 中元素 不是 上升的。
  • [3, 2, 5] 中元素 不是 连续的。

示例 2：

输入：nums = [2,2,2,2,2], k = 4

输出：[-1,-1]

示例 3：

输入：nums = [3,2,3,2,3,2], k = 2

输出：[-1,3,-1,3,-1]

提示：

  • 1 <= n == nums.length <=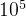 10^{5}
  • 1 <= nums[i] <= 10^{6}
  • 1 <= k <= n

解法一：通过连续上升的长度判断

  • 初始化：

    • ans 数组用于存储每个长度为 k 的子数组的能量值，初始时设置所有值为 -1，因为默认情况下每个子数组的能量值是 -1。
    • cnt 用来记录当前子数组中连续上升的元素的个数。

  • 遍历数组：

    • 对于每个位置 i，我们检查 nums[i] 是否是连续上升序列的一部分。如果是，cnt 增加 1；如果不是，cnt 重置为 1。
    • 如果当前连续上升的元素数 cnt 达到 k，则说明当前位置的子数组 nums[i-k+1...i] 满足连续上升条件，并且它的能量值是当前的最大值，即 nums[i]。
    • 然后将该子数组的能量值保存在 ans[i - k + 1] 中。

  • 返回结果：

    • 最后返回结果数组 ans，它包含每个长度为 k 的子数组的能量值。

Java写法：

  1. class Solution {
  2.     public int[] resultsArray(int[] nums, int k) {
  3.         // 获取数组长度
  4.         int n = nums.length;
  5.         // 初始化结果数组，默认值为 -1
  6.         int[] res = new int[n - k + 1];
  7.         // 初始化数组 res 所有元素为 -1
  8.         Arrays.fill(res, -1);  
  9.         
  10.         // upLen 用来记录当前连续上升序列的长度
  11.         int upLen = 0;
  12.         
  13.         // 遍历数组
  14.         for (int i = 0; i < n; i++) {
  15.             // 判断当前位置 nums[i] 是否是连续上升序列的一部分
  16.             // 如果是，upLen 增加 1；如果不是，upLen 重置为 1
  17.             if(i == 0 || nums[i] - nums[i - 1] != 1){
  18.                 upLen = 1;
  19.             }else{
  20.                 upLen++;
  21.             }
  22.             // 如果当前连续上升的元素个数达到 k，更新对应子数组的能量值
  23.             if (upLen >= k) {
  24.                 // 将该子数组的能量值（即最大元素 nums[i]）保存在 res 中
  25.                 res[i - k + 1] = nums[i];
  26.             }
  27.         }
  28.         // 返回结果数组
  29.         return res;
  30.     }
  31. }

C++写法：

  1. #include 
  2. #include   // for std::fill
  3.  
  4. class Solution {
  5. public:
  6.     std::vector<int> resultsArray(std::vector<int>& nums, int k) {
  7.         // 获取数组长度
  8.         int n = nums.size();
  9.         // 初始化结果数组，默认值为 -1
  10.         std::vector<int> res(n - k + 1, -1);
  11.  
  12.         // upLen 用来记录当前连续上升序列的长度
  13.         int upLen = 0;
  14.  
  15.         // 遍历数组
  16.         for (int i = 0; i < n; i++) {
  17.             // 判断当前位置 nums[i] 是否是连续上升序列的一部分
  18.             // 如果是，upLen 增加 1；如果不是，upLen 重置为 1
  19.             if (i == 0 || nums[i] - nums[i - 1] != 1) {
  20.                 upLen = 1;
  21.             } else {
  22.                 upLen++;
  23.             }
  24.  
  25.             // 如果当前连续上升的元素个数达到 k，更新对应子数组的能量值
  26.             if (upLen >= k) {
  27.                 // 将该子数组的能量值（即最大元素 nums[i]）保存在 res 中
  28.                 res[i - k + 1] = nums[i];
  29.             }
  30.         }
  31.  
  32.         // 返回结果数组
  33.         return res;
  34.     }
  35. };

 相比与Java写法的差别

  • vector：在 C++ 中，我们用 std::vector 来代替 Java 中的数组，vector 是 C++ 中的动态数组容器。
  • std::fill：在 Java 中，我们使用 Arrays.fill 来填充数组，C++ 中对应的操作是 std::fill，不过在这里我们直接在初始化 vector 时提供了默认值 -1，因此不需要额外的 std::fill。
  • 数组大小：在 C++ 中，通过 nums.size() 获取数组的大小，n - k + 1 是结果数组的大小，表示有多少个长度为 k 的子数组。
  • 逻辑保持一致：其余的逻辑完全保留 Java 中的思路，主要是遍历数组，判断每个子数组是否满足“递增”条件，并更新结果数组。

运行时间

时间复杂度和空间复杂度

时间复杂度：

  1. 遍历数组：
    主要的操作是在遍历 nums 数组。遍历 nums 数组的时间复杂度是 O(n)，其中 n 是数组的长度。

  2. 更新结果数组：
    更新 res[i - k + 1] 的操作是常数时间操作 O(1)。每次更新时，我们只做简单的赋值操作。

因此，总的时间复杂度是 O(n)，其中 n 是输入数组 nums 的长度。

空间复杂度：

  1. 结果数组：
    需要一个大小为 n - k + 1 的数组 res 来存储最终结果。该数组的空间复杂度是 O(n - k + 1)，即 O(n)（因为 n - k + 1 的量级与 n 相同，忽略常数项）。

  2. 其他变量：
    除了结果数组，还使用了几个常数空间的变量（如 upLen 和 i）。这些是常数空间 O(1)。

因此，总的空间复杂度是 O(n)，因为主要的空间消耗来自结果数组 res。

解法二：双指针+极限优化

优化前

  • 双指针定义：

    • left 指针指向当前窗口的左边界，right 指针指向当前窗口的右边界。
    • 初始时，left = 0，right = k - 1，表示窗口包含了从 nums[0] 到 nums[k-1] 的元素。

  • 滑动窗口：

    • 每次通过右指针 right 来扩展窗口，在窗口内用指针 p 来判断该子数组是否是一个连续的上升序列。
    • 如果是连续的，结果数组 res[left] 记录下该子数组的最大值（即 nums[right]）。
    • 如果不是连续的，res[left] 标记为 -1。

  • 窗口后移：

    • 每次判断完一个窗口后，左指针 left 和右指针 right 都向右移动一位，继续判断下一个子数组。

Java写法：

  1. class Solution {
  2.     public int[] resultsArray(int[] nums, int k) {
  3.         // k是大于1小于n的选手，我们直接诶采用双指针
  4.         int left = 0;
  5.         int right = k - 1;
  6.         int n = nums.length;
  7.         int[] res = new int[n - k + 1];
  8.         // 1,2,3,4,3,2,5
  9.         // l   r
  10.         while(right < n){
  11.             int p = right;
  12.             // 使用p指针判断区间是否为连续的
  13.             boolean flag = true;
  14.             while(flag && p > left){
  15.                 // 如果不是连续的直接结束并标记flag
  16.                 if(nums[p] - nums[p - 1] != 1){
  17.                     flag = false;
  18.                     break;
  19.                 }
  20.                 // 没事就继续往下判断
  21.                 p--;
  22.             }
  23.             if(flag){
  24.                 // 证明是连续的,放入最大值
  25.                 res[left] = nums[right];
  26.             }else{
  27.                 // 否则标记为-1
  28.                 res[left] = -1;
  29.             }
  30.             // 窗口区间后移
  31.             left++;
  32.             right++;
  33.         }
  34.         return res;
  35.     }
  36. }

优化前运行时间

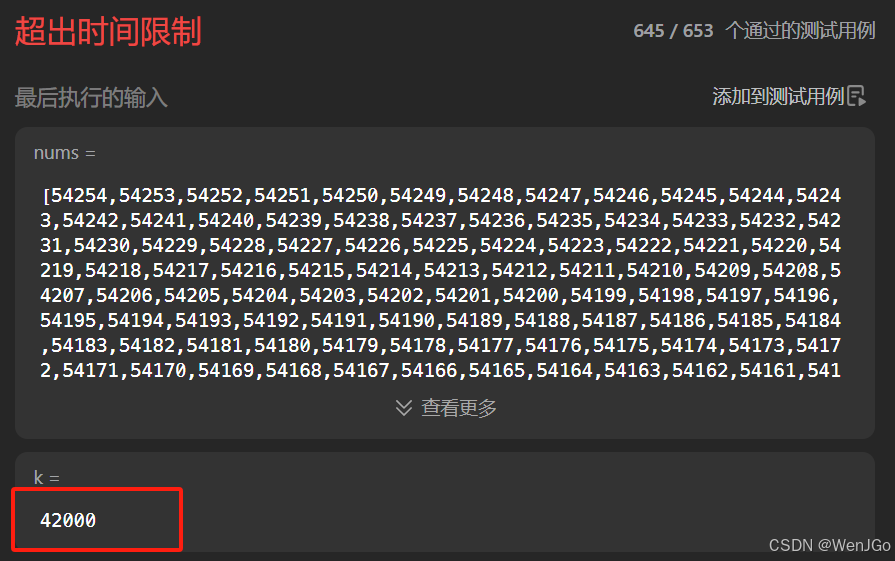
        显然是没有通过的，那么我们就进入优化操作吧。

优化后

        我采用了标记变量 isOK 和 oldRight 来控制和优化窗口的滑动逻辑。具体优化的地方主要在于减少大量不必要的判断和重复的计算。

优化的思路与实现：

  1. isOK 标志位：

    • 你引入了 isOK 标志变量，用来判断当前的窗口是否满足是连续上升的状态。如果是连续的，就可以直接根据 oldRight（即上一个窗口的右端）来判断是否继续。如果连续，就可以跳过一些不必要的计算，减少了重复的检查。

  2. oldRight 的使用：

    • oldRight 用来记录上一个窗口右边界的元素值。当当前窗口的右边界的元素与 oldRight 连续时，直接跳过重复计算，直接赋值并移动窗口指针。

  3. 判断子数组是否是连续的：

    • 当 nums[right] - nums[left] != k - 1 时，直接返回 -1，标记当前子数组不符合条件，减少了不必要的判断。

  4. 通过 flag 判断连续性：

    • 内部的 while(flag) 判断窗口内是否是连续上升的子数组，如果是连续的，就将最大值（即 nums[right]）保存到结果数组中。

Java写法：

  1. class Solution {
  2.     public int[] resultsArray(int[] nums, int k) {
  3.         // k是大于1小于n的选手，我们直接诶采用双指针
  4.         int left = 0;
  5.         int right = k - 1;
  6.         int n = nums.length;
  7.         int[] res = new int[n - k + 1];
  8.  
  9.         boolean isOK = false;
  10.         int oldRight = -1;
  11.         // 1,2,3,4,3,2,5
  12.         // l   r
  13.         while(right < n){
  14.             if(isOK && nums[right] - oldRight == 1){
  15.                 res[left] = nums[right];
  16.                 // System.out.print("是我" + nums[right]);
  17.                 oldRight = nums[right];
  18.                 // 窗口区间后移
  19.                 left++;
  20.                 right++;
  21.                 continue;
  22.             }
  23.  
  24.             oldRight = nums[right];
  25.             int p = right;
  26.             // 使用p指针判断区间是否为连续的
  27.             boolean flag = true;
  28.  
  29.             if(nums[right] - nums[left] != k - 1){
  30.                 res[left] = -1;
  31.                 // 窗口区间后移
  32.                 left++;
  33.                 right++;
  34.  
  35.                 isOK = false;
  36.                 continue;
  37.             }
  38.  
  39.             while(flag && p > left){
  40.                 // 如果不是连续的直接结束并标记flag
  41.                 if(nums[p] - nums[p - 1] != 1){
  42.                     flag = false;
  43.                     break;
  44.                 }
  45.                 // 没事就继续往下判断
  46.                 p--;
  47.             }
  48.             if(flag){
  49.                 // 证明是连续的,放入最大值
  50.                 res[left] = nums[right];
  51.                 isOK = true;
  52.             }else{
  53.                 isOK = false;
  54.                 // 否则标记为-1
  55.                 res[left] = -1;
  56.             }
  57.             // 窗口区间后移
  58.             left++;
  59.             right++;
  60.         }
  61.         return res;
  62.     }
  63. }

C++写法：

  1. #include 
  2. using namespace std;
  3.  
  4. class Solution {
  5. public:
  6.     vector<int> resultsArray(vector<int>& nums, int k) {
  7.         int n = nums.size();
  8.         vector<int> res(n - k + 1, -1);  // 初始化结果数组，默认为-1
  9.         
  10.         int left = 0, right = k - 1;
  11.         
  12.         // 滑动窗口从左到右移动
  13.         while (right < n) {
  14.             int p = right;
  15.             bool flag = true;
  16.             
  17.             // 判断当前窗口是否为连续的上升序列
  18.             while (flag && p > left) {
  19.                 if (nums[p] - nums[p - 1] != 1) {
  20.                     flag = false;
  21.                     break;
  22.                 }
  23.                 p--;
  24.             }
  25.             
  26.             if (flag) {
  27.                 // 如果是连续的，存储当前窗口的最大值，即 nums[right]
  28.                 res[left] = nums[right];
  29.             } else {
  30.                 // 如果不是连续的，标记为-1
  31.                 res[left] = -1;
  32.             }
  33.             
  34.             // 窗口后移
  35.             left++;
  36.             right++;
  37.         }
  38.         
  39.         return res;
  40.     }
  41. };

优化分析：

  1. 减少重复计算：

    • 通过 isOK 标志位和 oldRight 变量，避免了对已满足条件的窗口的重复检查，提升了效率。

  2. 减少无效窗口判断：

    • 如果当前子数组不符合连续上升的条件（nums[right] - nums[left] != k - 1），直接标记为 -1，并跳过后续的连续性判断，减少了不必要的计算。

  3. 提高效率：

    • 通过引入 isOK 标志，避免了对窗口中已满足条件部分的重复计算，提高了整体的处理速度。

运行时间

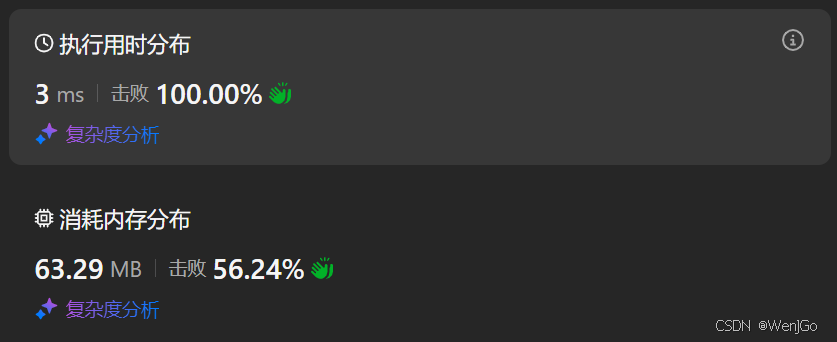
时间复杂度和空间复杂度

时间复杂度：

  • 外层 while (right < n)：这个循环会遍历所有可能的窗口，每次窗口后移 1，最多运行 n - k + 1 次。
  • 内层 while(flag && p > left)：在最坏的情况下，内层循环最多会执行 k - 1 次（即窗口的最大长度）。因此，内层循环时间复杂度为 O(k)。

最终的时间复杂度是 O(n * k)，和之前的复杂度相似。

空间复杂度：

  • 主要空间消耗来自结果数组 res，其大小为 n - k + 1，所以空间复杂度为 O(n - k + 1)，即 O(n)。

 

总结

      那么我们就成功的解决连续上升子数组能量值问题的两种解法，并提供了 Java 和 C++ 代码实现。问题要求对于一个数组 nums，找到每个长度为 k 的子数组是否是连续上升的，如果是，则记录该子数组的最大值，否则标记为 -1。

解法一：通过连续上升的长度判断

  1. 思路：遍历数组，用 upLen 记录当前连续上升的元素个数。当 upLen 达到 k 时，记录该子数组的最大值到结果数组。
  2. 优点：简单，时间复杂度 O(n)，空间复杂度 O(n)。
  3. 实现：使用 Java 和 C++ 语言实现，逻辑相同，使用 std::vector 或数组来存储结果。

解法二：双指针 + 极限优化

  1. 思路：通过双指针 left 和 right 滑动窗口来判断每个子数组是否是连续上升的。引入 isOK 标志和 oldRight 来优化判断，减少不必要的计算。
  2. 优化：通过提前判断连续性，避免重复计算，提升效率。若当前子数组不满足条件，直接标记为 -1，跳过后续计算。
  3. 时间复杂度：O(n * k)，与解法一相似，但减少了重复判断。
  4. 空间复杂度：O(n)，空间消耗主要来自结果数组。

对比：

  • 解法一适合简单情况，容易实现，但效率较低。
  • 解法二通过优化滑动窗口的判断，减少了不必要的计算，提升了效率，适用于更大的输入数据。

注：本文转载自blog.csdn.net的WenJGo的文章"https://blog.csdn.net/DDDDWJDDDD/article/details/143605075"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！