目录

一、前言

二、正文

1.和为k的子数组

1.1  题目解析

1.2  算法原理

1.3  具体代码

2.和可被k整除的子数组

2.1  题目解析

2.2  算法原理

​编辑

2.3  具体代码

三、结语

一、前言

        本文将继续为小伙伴们带来前缀和的学习，希望大家能够从中有所收获呀！！！

二、正文

1.和为k的子数组

1. 和为 K 的子数组 - 力扣（LeetCode）

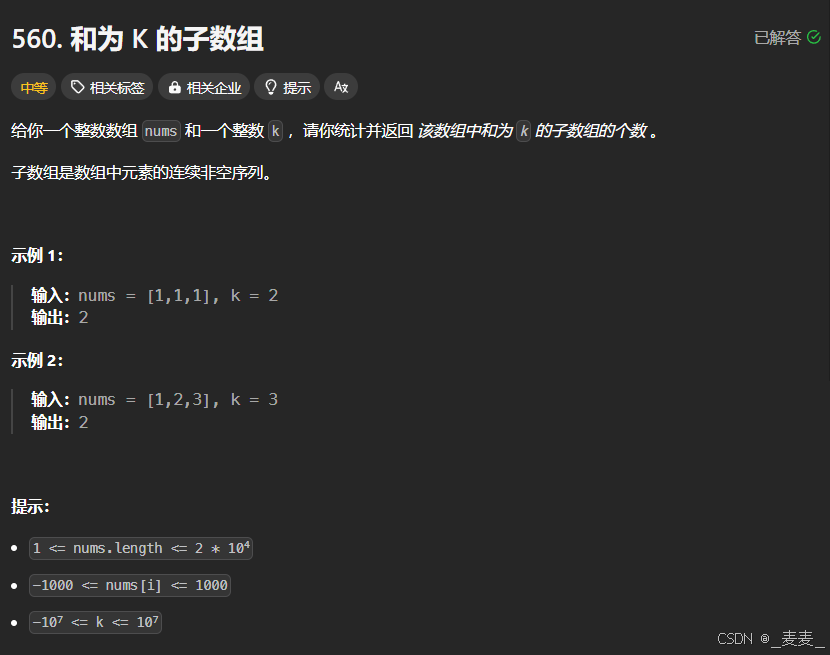
1.1  题目解析

        本题要求我们能够从所给整数数组中，统计所有子数组中所有元素和为k的次数

1.2  算法原理

        本题如果用暴力解法，就需要我们对数组中所有的子数组进行一一枚举并统计和是否k，时间复杂度为O（n²）。但是本题还有另一种解法，就是利用前缀和结合哈希表，乍一看可能小伙伴们觉得前缀和怎么和这道题能联系起来，其实需要我们对本题的求解进行一个转化。

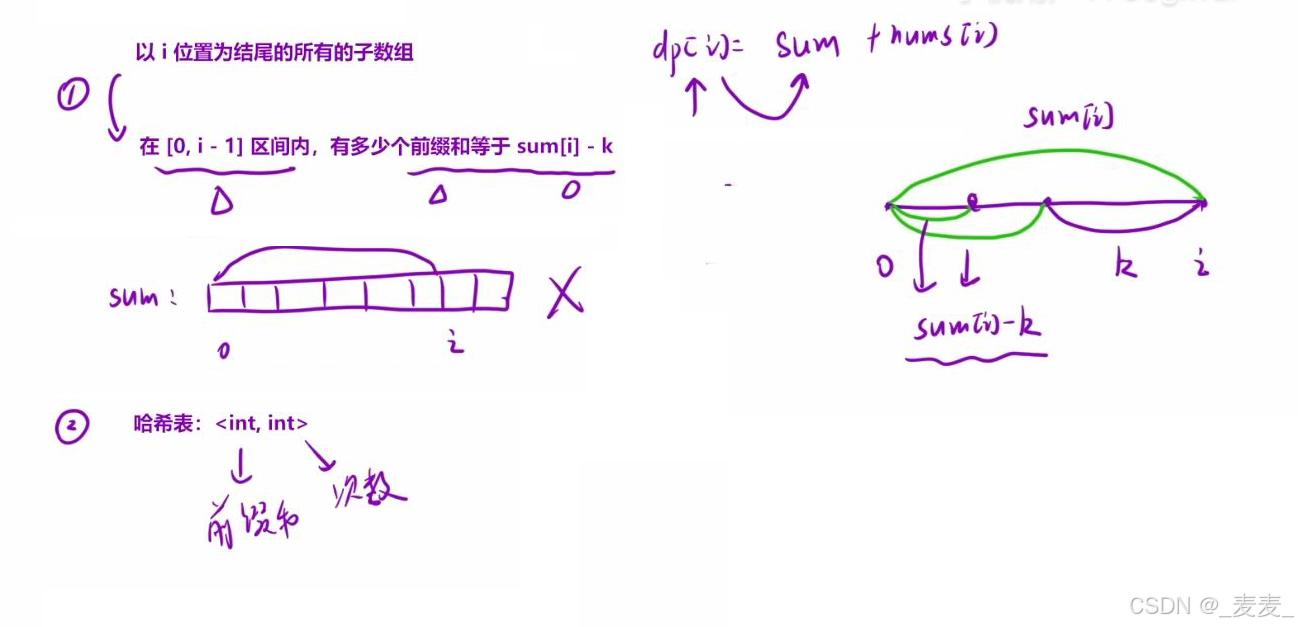
        这个转化就是题目要求我们求一个子数组和为k，也就是当我们计算以i位置为结尾的的子数组合条件的时候，其实我们只需要看前面有多少个前缀和满足当前i位置的前缀和sum【i】-k，该次数就是所有以i位置为结尾的所有子数组的和，为了统计前缀和出现的次数，我们用一个哈希表来记录，时间复杂度为O（n）。

代码细节：

①前缀和插入哈希表的时候应该是在计算i位置之前，也就是在计算i位置之前，哈希表中只保存【0，i-1】位置的前缀和，而不是像之前一样我们先预处理玩所有的前缀和，再进行后续的处理，这是为了避免我们在计算以i位置结尾的子数组时，把i位置后面的前缀和也考虑进去

② 我们无需创建一个前缀和数组，因为在我们统计的时候我们只用到了i位置前一个位置的前缀合即sum[i-1]，sum[i-1]+nums[i]即为sum[i]，因此我们只需要用一个sum变量来标记前一个位置的前缀和即可

③当我们在求前缀和sum【i】-k的次数时，有可能遇到当前sum【i】=k的情况，这时候所需前缀和应为0，所以我们在统计的时候应该在哈希表中插入前缀和为0的情况，为了不遗漏sum【i】=k这一情况

1.3  具体代码

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int sum=0,ret=0,n=nums.size();
        unordered_map<int,int> hash;    //统计前缀和出现的次数
        hash[0]=1;
 
        for(int i=0;i<=n-1;i++)
        {
            sum+=nums[i];
            ret+=hash[sum-k];
            hash[sum]++;
        }
        return ret;
    }
};

2.和可被k整除的子数组

2. 和可被 K 整除的子数组 - 力扣（LeetCode）

2.1  题目解析

        本题与上题略有所不同，要我们从题目中所给数组中统计出来所有和可被K整除的子数组

2.2  算法原理

        对于本题，来说依旧存在暴力解法，即枚举所有子数组的和，并判断是否能被K整除，时间复杂度为O（n²），但是利用前缀和加哈希表我们就可以将时间复杂度降为O(n)。依旧是利用转换的思想，我们要求以i为结尾的子数组能够整除K，就是求【0，i-1】区间内能够多少个前缀和能够整除K，同样的，为了统计前缀和的次数我们用一个哈希表来记录。

代码细节：

①前缀和插入哈希表的时候应该是在计算i位置之前，也就是在计算i位置之前，哈希表中只保存【0，i-1】位置的前缀和，而不是像之前一样我们先预处理玩所有的前缀和，再进行后续的处理，这是为了避免我们在计算以i位置结尾的子数组时，把i位置后面的前缀和也考虑进去

② 我们无需创建一个前缀和数组，因为在我们统计的时候我们只用到了i位置前一个位置的前缀合即sum[i-1]，sum[i-1]+nums[i]即为sum[i]，因此我们只需要用一个sum变量来标记前一个位置的前缀和即可

③为了应对sum【i】能够整除K这一情况，我们在统计次数前，先往哈希表中插入前缀和为0

补充知识：

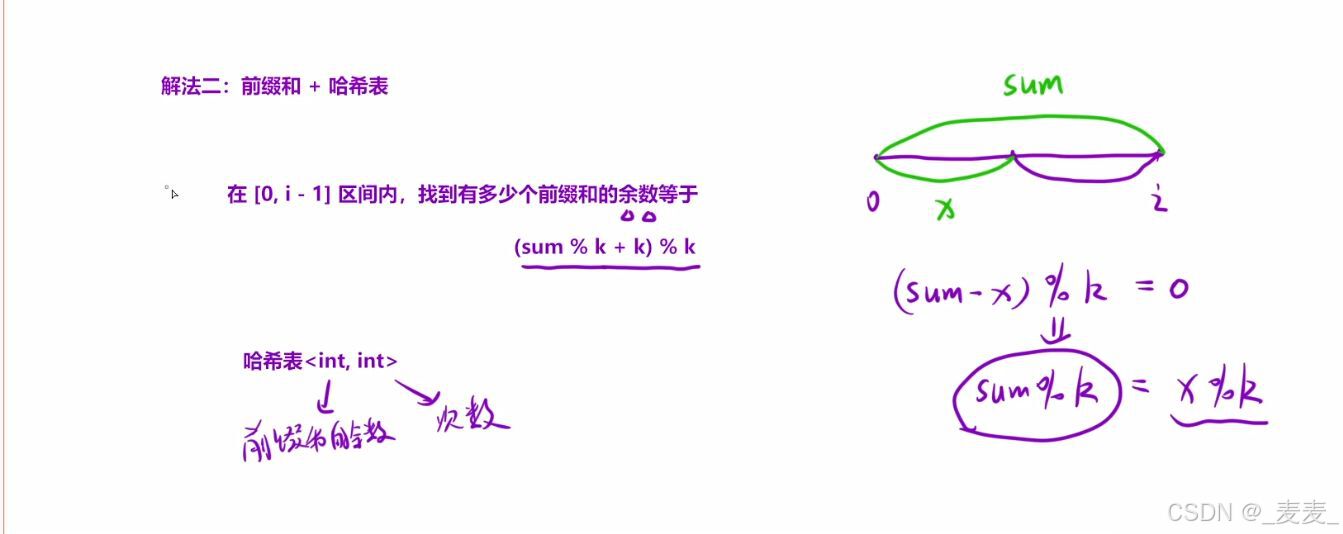
①同余定理，为什么求【0，i-1】区间内能够多少个前缀和能够整除K与以i为结尾的子数组能够整除K是等价的，这是因为由于同余定理告诉我们（a-b）/p=k余0可得出a%p=b%p，在本题中也就是本来是（sum-x）%k=0得出sum%k=x%k，x即【0，i-1】区间的前缀和

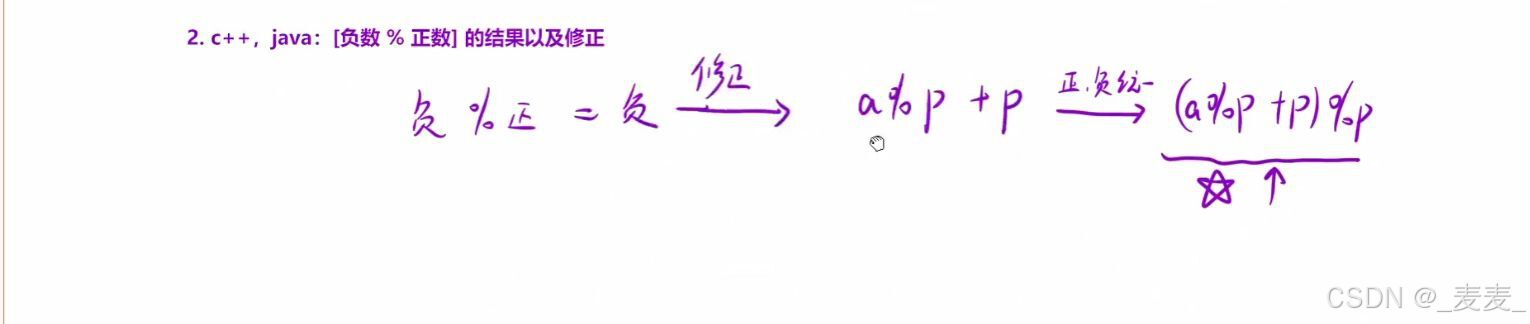
②负数%正数的修正，由于本题中数组的元素存在负数，因此前缀和可能出现负数的情况，所以在前缀和进行取摩的时候，我们需要进行修正，在C++中负数对正数取摩的修正是(原数%p+p)%p

2.3  具体代码

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        unordered_map<int,int> hash;
        int n=nums.size(),sum=0,ret=0;
        hash[0]++;  //0 这个数的余数
        
        for(int i=1;i<=n-1;i++)
        {
            sum+=nums[i]; // 算出当前位置的前缀和
            ret+=hash[(sum%k+k)%k]; // 修正后的余数并统计结果
            hash[(sum%k+k)%k]++;    //
        }
        return ret;
    }
};

三、结语

        到此为止，本文关于前缀和（三）内容到此结束了，如有不足之处，欢迎小伙伴们指出呀！

         关注我 _麦麦_分享更多干货：_麦麦_-CSDN博客

         大家的「关注❤️ + 点赞? + 收藏⭐」就是我创作的最大动力！谢谢大家的支持，我们下期见！

        欢迎大家参观我的算法专栏：麦麦的算法专栏